Series Convergence Tests Part II

Integral Test: The series can be compared to an integral to establish convergence or divergence. Let f(n) = a_n be a positive and monotone decreasing function. If then the series converges. But if the integral diverges, then the series does so as well.

Limit comparison test: If , and the limit exists and is not zero, then converges if and only if converges.

Alternating series test: Also known as the Leibniz criterion, the alternating series test states that for an alternating series of the form 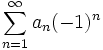math alternating series , if is monotone decreasing, and has a limit of 0, then the series converges.

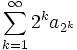Cauchy condensation test: If is a monotone decreasing sequence, then converges if and only if maths series cauchy condensation test condition converges.

[ Convergence Tests Part III ]